←   12. Esőben                                         14. Pontosság   →




13. Fuldokló kimentése



    Szerencsére nem túl gyakran kell vízparton fuldoklót kimentenünk (bár egy szép leányért bármit megtesznek a gimisek és az egyetemisták ...).   És ha a szántás mellett az aszfalton biciklizünk, és a szántásban / kukoricásban tetszik meg hirtelen valami (vagy rabló bújik meg)? Számtalan esetben lehet szükségünk az alábbi eredményekre!
    Épp a parton vagyunk tehát, futunk egy darabig, majd ha már "elég közel vagyunk" a célhoz, akkor vízbeugrunk. Minden igyekezetünk ellenére az úszás lassabban megy, de ha csak kb. kétszer-háromszor futunk gyorsabban, mint ahogyan úszunk, már nem biztos, hogy egészen a "célig" kell futnunk, azaz a partra merőlegesen kell úsznunk. (Az ábrán ezt φ -vel jelöltük.)



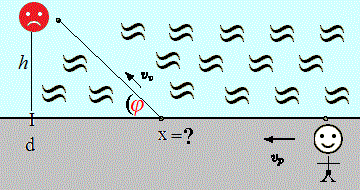
    Időt nyerhetünk azzal ugyanis, ha már előbb ugrunk, hiszen a felesleges továbbfutással csak időnk telik. (A kifáradással most nem törődünk, hiszen fiataloknál ilyen nincs.)
    Az idő kiszámítását és az optimális ugrási hely (x) matematikai (vagy kísérleti?) megkeresését egy középiskolás vagy egyetemista könnyedén elvégzi, vagy a csatolt Megoldás fájlban megtalálja.
    Az optimális ugrási hely (x) képlete ugyan elég bonyolult, de érdekes módon az úszás és a futás által bezárt szög (φ) egyedül a két sebesség hányadosától függ:

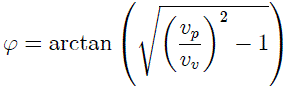
A fenti képlet azt jelenti, hogy φ CSAK a sebességek arányától függ. Tehát elegendő otthon előre lemérnünk futásunk és úszásunk sebességeinek arányát, és a fenti képlet vagy a Megoldás -ban található táblázat alapján már csak φ értékét kell megjegyeznünk. A parton pedig mindenféle számolás nélkül (de egy szögmérővel a fürdőnadrágunkban) már futhatunk is! Addig kell futnunk, míg a part és a fuldoklóhoz húzott egyenesek által bezárt szög éppen φ lesz, és ekkor kell a vízbe vetnünk magunkat! (A vvíz=vpart esetet külön kell vizsgálni, ez már az Olvasó feladata!)

   
  http://www.amazon.de/K%C3%B6nnen-Hunde-rechnen-Norbert-Herrmann/dp/3486580213

    Norbert Herrmann (Universität Hannover) matematikus könyvében (Tudnak a kutyák számolni?) az alábbiakat olvashatjuk:



    "Kísérletekkel meggyőződtek arról, hogy a kutyák minden esetben az optimális (x) helyen, vagyis az optimális φ alatt ugrottak a vízbe össze-vissza dobott cél (fadarab) után. "   Természetesen minden kutyánál más lehet a sebességek vvíz/vpart aránya, ezt is megmérték a kutatók. És láss csodát: mindegyik kutya "tudta" (ösztönösen?) saját vvíz/vpart arányát, vagyis saját optimális φ szögét!


Játsszunk egy kicsit!

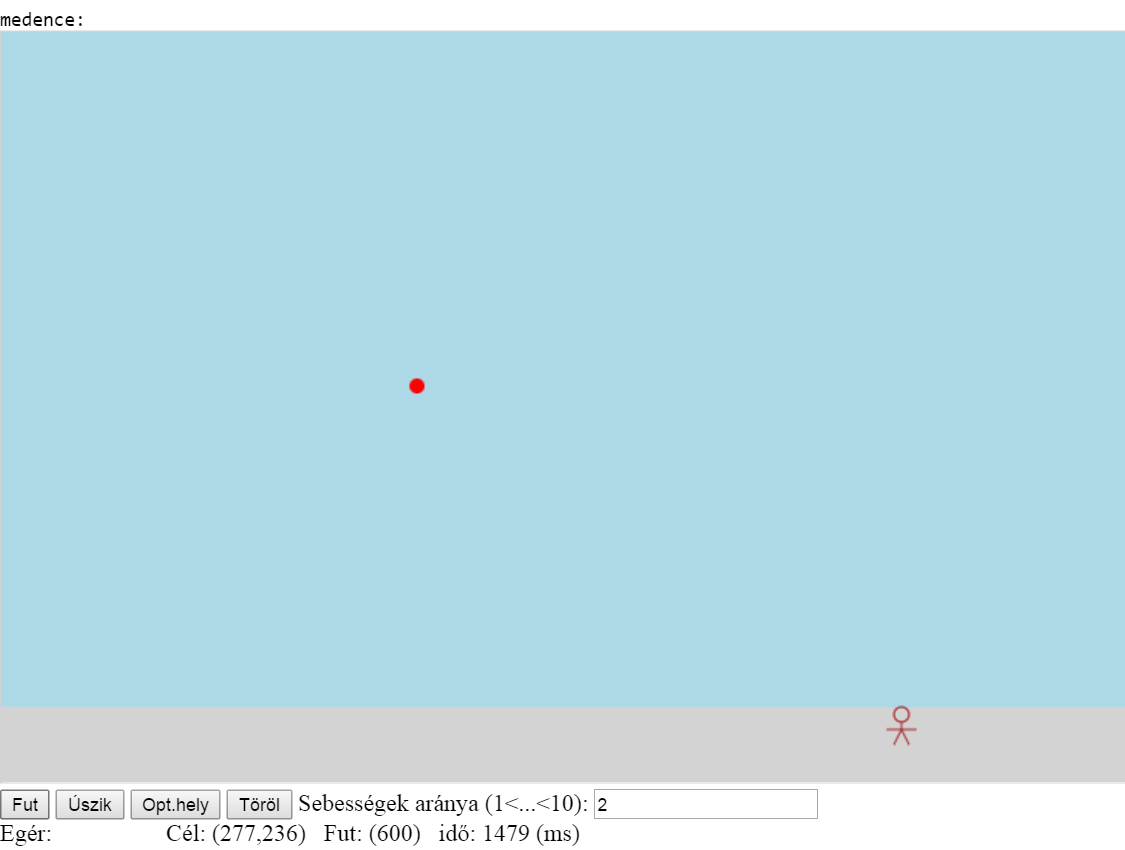
    A mellékelt kis programban fejleszthetjük ügyességünket: mekkora sebességgel kell futnunk és hol kell vízbeugranunk. (Stopperórát mellékeltem, a program kérésre az optimális helyet és a szöget is kijelzi.)



    Egy kicsivel bonyolultabb (és életszerűbb) feladat, ha nem a part mentén kell futnunk, hanem a homokozónál állva vesszük észre másik gyermekünk "Apúúúú! Hozd vissza a labdám!" visítását:



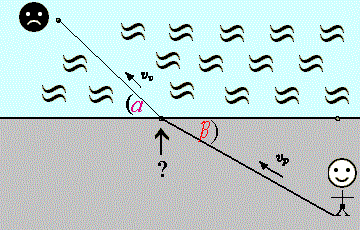
    A részletes számításokat most nem mellékeljük, ezt minden I. évfolyamos egyetemistának a vizsgán illik tudni levezetni. (A megoldást elovashatjuk például Koltay László és a Szerző         Analízis I. feladatgyűjteményében, aminek tartalomjegyzékét a Szerző honlapján találhatjuk meg.)
    A végeredmény egyszerű és meglepő: az optimális vízbeugrás feltétele:

sin(90°-α) / sin(90°-β) = vv / vp .

Ismerős ez a képlet! A fénytörésnél tanultuk: különböző anyagok határfelületénél a fény megtörik, a fenti képlet pedig a fénytörés képlete! Hát persze! Különböző anyagokban a fény sebessége különböző, és mivel a fény a legrövidebb idő alatt szeretne egyik helyről a másikba jutni, ezért ugyanúgy viselkedik, mint a kutyák! (A fizikakönyvekben csak azért van a   sin(α)/sin(β) = vv/vp   képlet, mert ott a beesési merőlegeshez képest mérik a szögeket, mi pedig a felületek határához, vagyis mi a fizikakönyvek kiegészítő szögeit jelöltük α ill. β betűkkel.)
←   12. Esőben                                         14. Pontosság   →




Szalkai István
Pannon Egyetem
Matematika Tanszék
Veszprém
szalkai@almos.uni-pannon.hu
2014.12.03.