Pontosság (Szalkai István)

← 13. Kimentés 15. Torzítás →

14. Pontosság

"Apu sohasem pontos, mindig nagyon későn jön haza!",
"A falazáson miért nem jó az a tenyérnyi lyuk? Egy kanál malter majd eltakarja!",
"Nahát! A pirinyó sejtbe be tudnak nyúlni a tudósok, és ki tudják cserélni a sejtmagot, vagy akár a DNS-molekulát is?! "

Igen, a pontosság viszonylagos! (Hányszor vártam én is szívem hölgyére félórákat!) Néha én is szenvedtem csipesszel a kinder-tojás mütyürökkel, de ha az ajtótábla nem akart a helyére csúszni, a kalapács is segített sokszor!
Mindennapi tevékenységeinket általában előre meg szoktuk tervezni, sokszor még számolunk is. Jó sokat, oda-vissza ellenőrzünk, de vajon pontos -e a végeredmény?

A számolás pontossága

A középiskolában még jó dolgunk van: a végeredményt "csak" két tizedesjegy pontossággal kérik. DE: Vajon elég-e már a számolás közben, minden lépésben csak kettő tizedesjegyre kerekítenünk a részeredményeket? A hibaszámítás hosszadalmas elmélete helyett inkább nézzünk egy tanulságos példát.

Oldd meg az alábbi egyenletrendszert (papíron, ceruzával és zsebszámológéppel), majd az ellenőrzéshez nyomd meg az "I.Megoldás" gombot:

I. Egyenletrendszer: i ) 5.0002*x - 3.7342*y = 12.1226 ii) 4.9997*x - 3.7339*y = 12.1224 ---------------------------------

A következő egyenletrendszer nagyon hasonlít az előzőhöz: az együtthatók alig pár tízezreddel térnek el az előző együtthatóktól. Mennyit változik a végeredmény? Becslés helyett vegyük elő ismét a zsebszámológépünket, és nagyon pontosan oldjuk meg ezt is (ellenőrzés a "II.Megoldás" gombbal):

II. Egyenletrendszer: i ) 5.0002*x - 3.7342*y = 12.1226 ii) 5.0004*x - 3.7344*y = 12.1228 ---------------------------------

Mi lehet az oka annak, hogy a fenti I. és II. , nagyon hasonló egyenletrendszerek megoldásai ennyire eltérőek: az együtthatók eltérése több, mint tízezerszeresére nőtt meg !!! Másképpen gondolkozva: ha az I. (vagy a II.) Egyenletrendszert már egy előzetes számolás után kapjuk, akkor az eddig elkövetett (pár tízezrednyi) hiba már rettenetesen elrontotta a végeredményünket! Mennyire ronthatja számolásunk (a végeredmény) pontosságát, ha minden lépésben kettő (négy,...) tizedesjegyre kerekítünk?

Az alábbi program segít a számolás pontatlanságának nyomon követésében.
Adj meg egy tetszőleges egyenletrendszert, add meg a számolás közben (végig) alkalmazandó "pontosságot" (vagyis minden lépésben hány tizedesjegyre kerekítsünk, 0 és 10 között), majd nyomd meg a "Számolás" gombot. Figyeld meg a végeredmény (és a köztes lépések) változását a pontosság többszöri módosítása után! (Ha kíváncsi vagy a bevezetőben említett egyenletrendszerek viselkedésére, elég az "I.Egyenletrendszer" ill. a "II.Egyenletrendszer" gombokat megnyomnod.)
Figyelem: az alábbi programban a₁ nem lehet nulla !

Megoldás:

Nem csak a fenti "kicsiszolt" egyenletrendszerek instabilak ennyire, hanem középiskolás fizika, kémia és egyéb tankönyvekben is sok olyan példát találunk, amelyek végeredménye csak akkor lesz két tizedesjegyre pontos, ha számolás közben minden lépésben legalább négy vagy hat jegyre számolunk pontosan!
Most csak két példát idézek Mindennapi matematika könyvemből (sajnos még kiadatlan):

A könyv tartalomjegyzékét a honlapomon megtalálhatjátok: Mindennapi matematika , mint az idézett hivatkozást is: Mesék a valószínűségszámításból .

A grafikon pontossága

A precíz (hosszadalmas) számolás helyett jobban szeretjük a szemléletes, "grafikus" megoldásokat. A számítógépek korában nagyszerű, pontos rajzolóprogramok között válogathatunk, főleg egyenesek metszéspontját ("Mi ez nekünk?") könnyedén megtalálhatjuk. A koordinátasíkon símán mozoghatunk, nagyíthatjuk, kicsinyíthetjük az ábrát, végül a metszéspontra az egeret csúsztatva a koordinátákat a program máris kijelzi, akár több tizedesjegy pontossággal!
Próbáljuk csak ki:

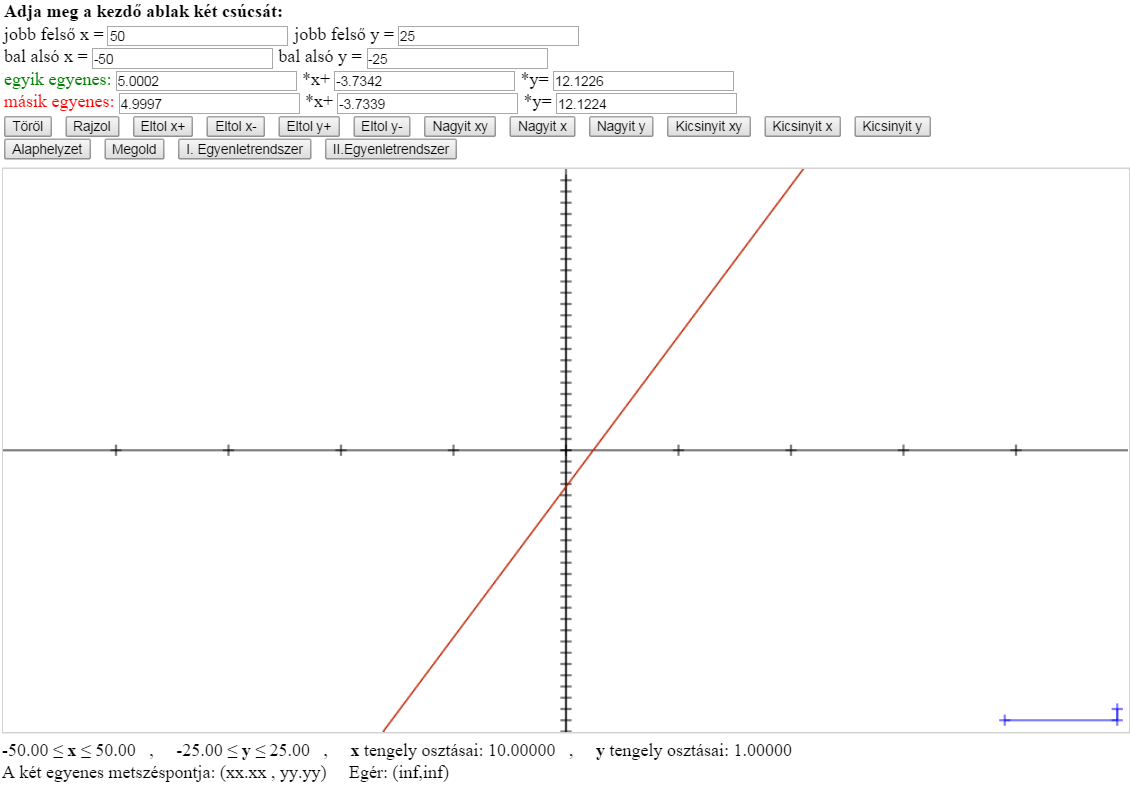
A bevezetőben megismert egyenletrendszereket ismét előhívhatjuk a programban a két utolsó (I. Egyenletrendszer és II. Egyenletrendszer) gombbal. Ha a megadott egyenesekkel nem boldogulunk, akkor próbálkozhatunk például a 3x+4y=5, 4x-3y=6 egyenespárral.

Kérdések, tapasztalatok:
1.) Miért torzít a rajz a Nagyit x , Nagyit y , Kicsinyít x és Kicsinyít y gombok után? De kérem! ha az egyik koordinátatengelynek változtatjuk a beosztását, nyilván az ábra is torzul! (Tudományosan ezt affinitásnak nevezik.) Gondoljuk csak meg: minden derékszögű háromszögnek változnak a szögei, ha befogóit nem egyforma mértékben változtatjuk! Ha lehet, használjuk tehát a Nagyit xy és Kicsinyít xy gombokat!
Másrészt, ha egymás után nyomjuk meg a Nagyit xy és a Kicsinyít xy gombokat (akármilyen sorrendben), akkor miért nem kapjuk vissza pontosan az előző képernyőt? Ugyanis mindkét gomb 10% -kal változtatja meg a koordináta-ablakot, és például 90% -nak 10%-a nem ugyanaz, mint az eredeti 100% -nak a 10% -a, ezért van az "elcsúszás". Használjunk minden számítógép-grafikát körültekintően!
Ezt a kérdést részletesebben tárgyaljuk a 15. Torzítás fejezetben.
2.) Miért nem látjuk soha mind a két egyenest az ábrán? Pedig kiszámoltuk pontosan a metszéspontot, és annak közelében nagyítgatunk! Ha csak arról lenne szó, hogy egyik egyenes "lelóg" a papírról, akkor előbb-utóbb megtalálnánk. Kedvenc egyenletrendszereink azonban majdnem párhuzamos egyenesekből állnak, ugye?! Ebből az következik, hogy kismértékű nagyítás esetén nem tudjuk őket megkülönböztetni, további nagyításkor azonban "hirtelen szétugranak": nem csak szétválnak, hanem le is "lökik" egymást a papírról.

Mesélek még egy kicsit a "majdnem párhuzamos" egyenesekről. Bizonyára mindannyian észrevettétek már, hogy egyenes vonalat hosszú ollóval szeretünk vágni, de annak csúcsánál már nehezebb a vágás, ha kicsit keményebb papírral van dolgunk.

Egyrészt a papír felőli erőkar nő, míg az ujjunk felőli nem változik, vagyis növelnünk kell izomerőnket a forgatónyomaték kiegyenlítéséhez. Ezzel összhangban van az egyenletrendszerekről most szerzett tapasztalatunk: nagy szögben érintkező egyeneseknél (bal oldali fénykép) kis változás esetén a metszéspont (a pengék vágásfelülete) csak kicsit "ugrik" (= kis munka), míg kis szögben érintkező egyeneseknél (jobb oldali fénykép) már pici változás esetén is nagyot "ugrik" a metszéspont, ami pedig nagy munka (út*erő).
Másrészt, egyenes vonal vágásához természetesen jó irányban kell tartanunk az ollót, vagyis meg kell becsülnünk (terveznünk) a vágás további menetét. Ez pedig a nyitott ollónál nehezebb, közepesen zárt ollónál a legegyszerűbb, majdnem összecsukott helyzetben célozni ugyan a legegyszerűbb, csak mi mozgatjuk a hosszú ollót. Ezt már Dobó István egri várkapitány is észrevette: ő az ágyúk végével céloztatott, és talált, míg a törökök az ágyúk elejével, és kevésbé pontosan találtak a célba!

← 13. Kimentés 15. Torzítás →

Szalkai István
Pannon Egyetem
Matematika Tanszék
Veszprém
szalkai@almos.uni-pannon.hu
2014.12.03.