← 11. Nyugaton
13. Kimentés →
12. Esőben autózunk
Igaz, hogy álló autóban az ablaktörlőt ki szoktam kapcsolni, de
mintha ekkor kevesebb eső is esne az elülső szélvédőre! (?) A nagy
kérdés tehát a következő: álló, vagy mozgó autó ablakára esik kevesebb eső?
(Természetesen szélcsendes időről van szó.)
Ha függőleges lenne az első ablak is (vagy esetleg előrefelé dűlő,
vagyis kifelé), akkor bizonyára igazam lenne, hiszen álló autó függőleges ablakára
semmi eső nem esik, elinduláskor pedig bizonyára "elütnék" néhány esőcseppet
az ablakkal! Talán a vízszintes tetőablak esetét még meg tudjuk jósolni: álló autónál
minden esőcsepp itt "landol", de ha esetleg jó gyorsan haladok, akkor mindegyik
esőcsepp alól kihúzom a kocsit, talán még egy sem esik rá! Mint a mesebeli katona,
aki esernyő helyett a kardját forgatta a feje fölött. (Különben is, a vízszintes a
függőleges ellentéte ...!) A függőleges hátsó ablak esete még egyszerűbb:
az ablakra semmi sem esik, sem álló, sem (előrefelé) mozgó autónál - talán épp ezért
is lesz olyan koszos az út végére. De ferde ablakokkal mi a helyzet?
"No, emiatt nem fogok lassítani/gyorsítani ... " modja
magában az Olvasó, és igaza van: vezessünk lassan esőben! "Az ablaktörlő
motort is mindenki egyéni tempóra állítja. Nem számolgatom a cseppeket, a matekot
még a piros lámpánál sem veszem elő!" - hallom a véleményeket. "...
valahány csepp esik rája, annyi áldás szálljon rája" - ez a lényeg!
Tehát általában is felvethetjük a kérdést:
Hogyan függ az ablakra eső cseppek száma az ablak dőlésszögétől, az autó
sebességétől és az eső intenzitásától? (Ez utóbbira egyszerű a válasz.)
Vizsgálhatjuk a be- és kifelé dűlő, valamint az első- és hátsó- ablakokat is, a
tetőablakot is, valamint az álló autó esetét is.
A számítások bonyolultaknak tűnnek (legalábbis első ránézésre),
ezért inkább próbáljuk jobban megfigyelni a jelenséget.
"Játsszunk" egy kicsit!
A
csatolt honlapon
található (játék)programmal tanulmányozhatjuk az autó szélvédőjének szöge,
az autó sebessége és az ablaküvegre csapódott esőcseppek száma közötti
összefüggést! Próbáljuk ki!

Balesetmentes kísérletezést!
Elméleti háttér
Most komoly matematika következik, de előtte töltődjünk fel egy
olyan dallal, amit autóban szoktam dúdolni zuhogó esőben:

Nem kell megijedni, nem fogunk bonyolult fejtegetésekbe bocsátkozni
(ezek a mellékelt Megoldás -ban megtalálhatók).
Az esőcseppek sebességét magunk is kiszámolhatjuk, de
kedvenc tanítóm, Öveges József bácsi könyveiben is megtalálhatjuk, például
 Élő fizika
Élő fizika
 könyvében, melyet sok-sok kiadásban megtalálhatunk, részletesebben lásd a
http://www.mora.hu/sorozat/oveges-konyvek címen.
könyvében, melyet sok-sok kiadásban megtalálhatunk, részletesebben lásd a
http://www.mora.hu/sorozat/oveges-konyvek címen.
Az esőcseppek apró méretük és a légellenállás miatt egyenletes sebességgel
esnek lefelé. Ha egy esőcsepp átmérője körülbelül 1 mm (R=0.0005m) és gömb alakú
(és vízből van), akkor a gravitációs erő. ami a vízcsepp súlya, pontosan
megegyezik a légellenállással:
4*0.00053*π/3 = 0.023*0.00052*π*v2
4*0.0005/3 = 0.023*v2
0.028 ≈ v2
0.17 ≈ v
tehát v ≈ 0.17 m/s. Ha a fenti számolásban minden lépésben kerekítünk,
a végeredmény 0.019m/s is lehet, a számolások pontatlanságáról a
14. Pontosság
fejezetben olvashatunk bővebben.
Tekintsük most az eredeti problémánkat: az esőcseppek és az
autóüveg találkozásait.
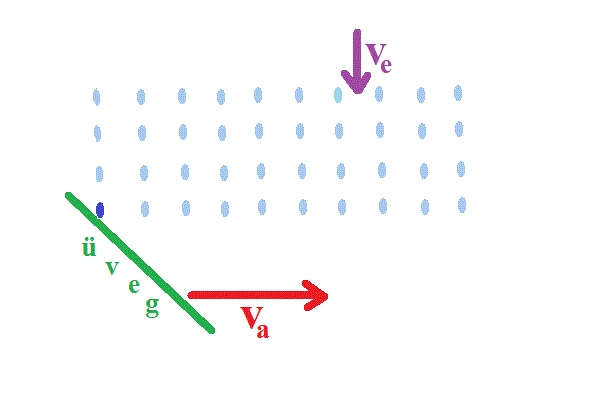
Egyszerre két mozgást a földről nézni és számítani (elemezni)
nehéz, ezért valamelyik mozgó tárgyról kell vizsgálnunk a jelenséget! Mi
most a mozgó autóban ülünk, vagyis az AUTÓ -hoz rögzített koordinátarendszerből
nézzük az esőcseppek mozgását. Az oldalsó ablakon (akár a hátsó ülésen, akár buszon
vagy vonaton) jól láthatjuk: álló járműben az esőcseppek szépen, függőlegesen esnek
lefelé. Ha pedig egyre gyorsabban haladunk, akkor az esőcseppek nyomai már nem
függőlegesek, hanem ferdék: mintha "hátrafelé" esnének, a dőlés szöge a
jármű sebességétől függ. A fizika órákon megtanultuk, hogy a sebesség
vektormennyiség, tehát az esőcseppek sebességéhez hozzá kell adni az autó
sebességének (-1) -szeresét, amint ezt a baloldali ábrán látjuk! Ugyanis
mi az autóban úgy érezzük, hogy mi állunk, vagyis az esőcseppek közelednek,
"visszafelé" jönnek felénk, a fekete vö nyíl irányában.
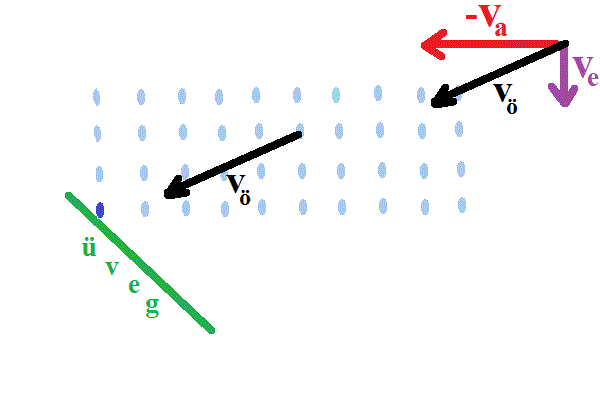

Csak azt kicsit nehéz elképzelni, pontosabban kiszámolni, hogy az
esőcsepp-tenger (kék pöttyök négyzetrács alakban) jön felénk, és az üvegtáblán
felfogott cseppeket kell megszámolnunk!
Sokkal jobban átlátható a probléma, ha az egész ábrát megfordítjuk:
az esőcseppek álló tengerében (kék pöttyök négyzetrács alakban) kell az ablaktáblát
mozgatnunk, és az elsöpört pöttyöket megszámolnunk, mint ez a jobboldali ábrán
látható. Az ablak most a zöld vö vektor
irányában mozog. (A fizikusok szerint mi most nem az autóban, hanem egy esőcseppen
ülünk, ezért látszik a többi esőcsepp is állni, és ezért látszik az autó felénk jönni
a vö vektor "irányából".)
Hány esőcseppet találunk el adott idő vagy megtett km alatt, és ez
a mennyiség hogyan függ az ablak dőlésszögétől és az autó sebességétől? Ez már kicsit
hosszabb számolás, a részletek a mellékelt Megoldás -ban
megtalálhatók. Kezünkbe vehetjük még J.B.Csernyak és R.M.Rose:
 A minszki csirke - Szemben az információs szupersztrádával
könyvét is (például:
http://www.libri.hu/konyv/jurij_b_csernyak.a-minszki-csirke.html),
amelyben ez és számos hasonló probléma megoldását részletezik a szerzők.
A minszki csirke - Szemben az információs szupersztrádával
könyvét is (például:
http://www.libri.hu/konyv/jurij_b_csernyak.a-minszki-csirke.html),
amelyben ez és számos hasonló probléma megoldását részletezik a szerzők.
Most csak annyit árulunk el, hogy az esőcseppek "terének fluxusában"
haladunk egy ablaküveggel, de szerencsére integrálnunk nem kell. Ami pedig a fenti
(játék)program megírásakor a legnehezebb volt: kiszámolni, hogy mely esőcseppek
és hová fognak az ablaküvegre esni:
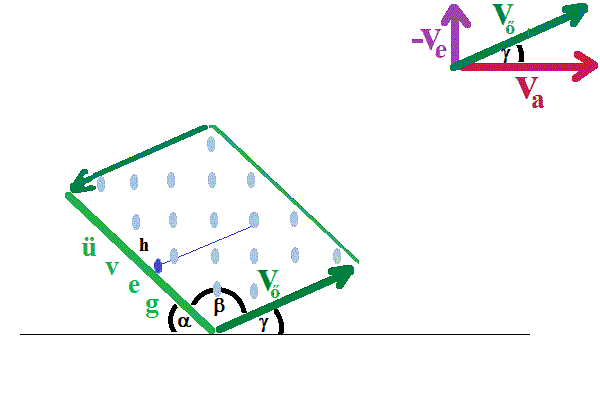
Egy kis lineáris algebrával (vektorok, egyenletrendszer, determináns) máris
megoldottuk! (Részletek: Megoldás .)
Erről jut eszembe: hallottatok -e már G.A.Pick tételéről: a
(derékszögű) koordinátarendszerben ha egy sokszög csúcsai rácspontok (mindkét
koordinátájuk egész szám), vagyis ez egy rács-sokszög, akkor területét
egyszerűen kiszámíthatjuk:
Pick Tétele: Ha egy rácssokszög belsejében
b , kerületén
k rácspont található, akkor területe
T = b + k/2 -1 :
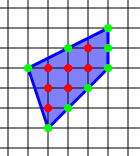
az ábrán: T=7+8/4-1=10
(
http://hu.wikipedia.org/wiki/Pick-t%C3%A9tel).
De miért látjuk a szembejövő esőcseppeket (főleg éjjeli megvilágításban,
ha első ülésen utazunk) ívelt pályán közeledni felénk, mintha egy parabolapálya
"alját" látnánk szemből - egészen ijesztő látvány esténként! Sem ezt a problémát, sem
az eredeti problémát a háromdimenziós térben lehetséges összes lehetséges módon
(vagyis előre-, hátulra- vagy netán oldalra dűlő első- vagy hátsó ablakkal utazni előre-,
hátra vagy netán oldalra, felfelé, ... irányban) most nem fogjuk már megoldani. Ennyi
nekem is elég volt.
Vezetéskor ne a matematikán vagy fizikán gondolkozzunk, hanem
figyeljünk a forgalomra! Balesetmentes vezetést!
← 11. Nyugaton
13. Kimentés →
Szalkai István
Pannon Egyetem
Matematika Tanszék
Veszprém
szalkai@almos.uni-pannon.hu
2014.12.03.







