←   16. A Föld gömbölyű                                         18. Fények és árnyak   →




17. Látószögek



    A legnagyobb

    "Mi is az a látószög? Már megint egy matematikai definíció!" - hallom dohogásodat kedves Olvasóm! Pedig egyszerű: a legkisebb olyan szög, amekkorára szemünket ki kell nyitnunk ahhoz, hogy a nézett tárgyat éppen lássuk, beleférjen látómezőnkbe:


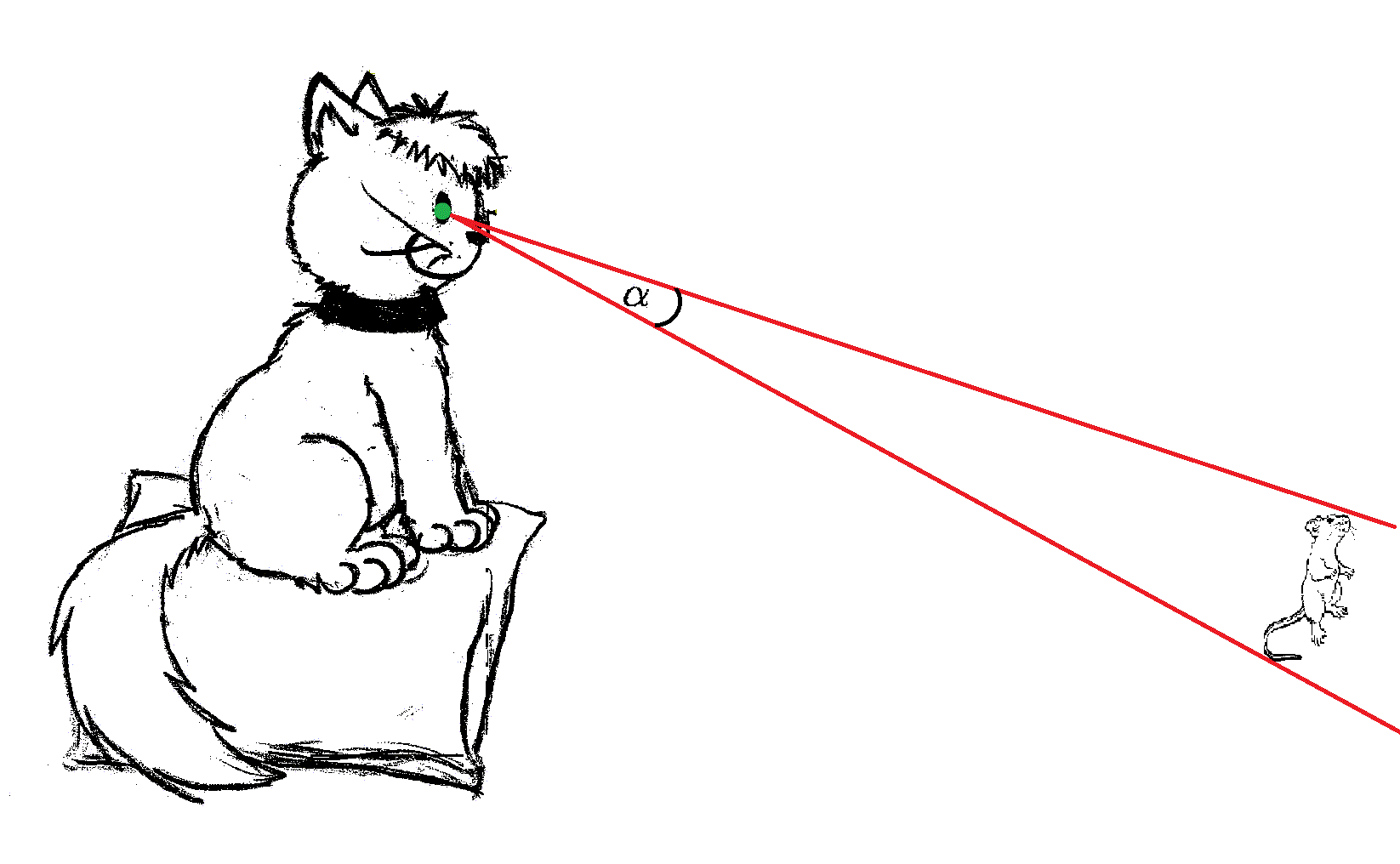
    Nyilván egy tárgyat akkor látunk nagyobbnak vagy kisebbnek, ha az aktuális nézőpontunkból a látószöge nagyobb vagy kisebb. A csillagok is ezért "pislognak" éjjelente: nagyon kicsi a látószögük, és a levegőben levő porszemek időnként eltakarják szemünk elől őket.
    Fényképezéskor, szemlélődéskor azért toporgunk és téblábolunk sokáig, mert a lehető legjobb nézőpontot, vagyis a legnagyobb látószöget szeretnénk "látni". (Távcső és mikroszkóp nem mindig van nálunk kiránduláskor vagy sportoláskor.) Legtöbbször ugyan nem sok választásunk van (szűk az utca vagy a terem, sok a járókelő), de azért érdemes egyszer megvizsgálni a lehetséges legjobb, optimális helyzeteket.

    Milyen esetekben lesz hasznos az alábbi matekóra?

   

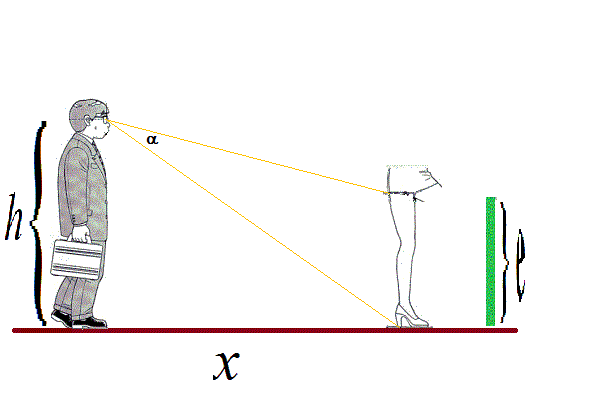
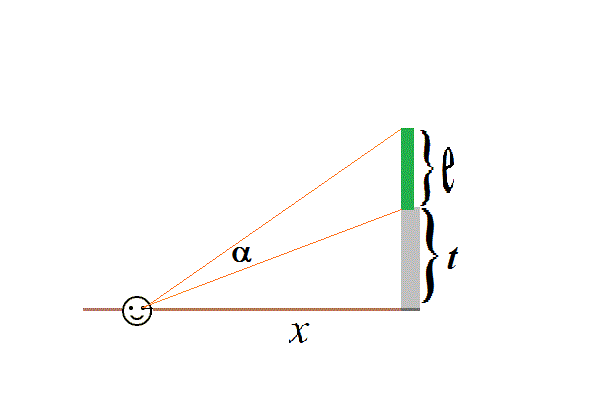
    Magas talapzaton vagy hegyen levő szobrot, épületet nézünk vagy fényképezünk. Ha túl közel vagyunk, akkor nem csak az a baj, hogy függőlegesen kell(ene) felfelé néznünk, hanem amúgy sesm látnánk sokat: túl kicsi (vagy 0) a látószög. Ha túl messze megyünk, szintén kicsi a látószög, tehát valahol "középen" van az arany megoldás. Ugyanez a helyzet, amikor egy kisgyerek az asztalon lát egy tárgyak (nem feltétlenül a TV-t), vagy, ami még szörnyűbb élmény számára: anyukáját sem közelről látja a legjobban, de akkor hogyan bújjon hozzá?
    A középső ábra, az úgynevezett láb-probléma nem szorul magyarázatra (h és l adott, keresendő x valahol középen). Repülőről is hasonló a gond: milyen x távolságból látjuk a legjobban az ellenség zöld színnel jelölt függőleges épületét?
    A harmadik ábrán a pálya szélén (barna csík), bedobáskor a helyét kereső focista a zöld kaput szeretné a lehető legnagyobb szög alatt látni. Hasonló a helyzet egyes múzeumi termekben: csak a terem szélén szabad sétálnunk, és a falon levő festményt (zöld téglalap) szeretnénk minél jobban látni. Az előadásra késve érkező színházlátogató (egyetemi hallgató is csak a terem szélén foglalhat helyet, a zöld színpadot vagy táblát más és más szögben látja a terem szélén (a barna vonalon).
    Vegyük észre, hogy mindhárom esetben az ábra ugyanaz: a két szélső esetben "felfelé" nézünk, a középső esetben "lefelé" :


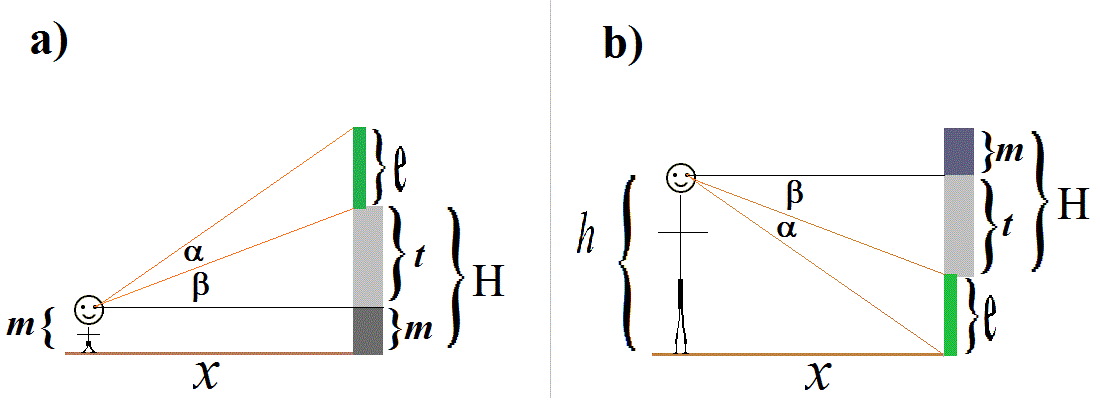
A b) ábrát a szemünk vonalában levő vízszintes egyenesre tükrözve éppen az a) ábrát kapjuk (és fordítva).
    A paraméterek (betűk), valamint a zöld "tárgy" és a barna vonal jelentése mindegyik felsorolt esetben ugye világos. x értékét mindegyik esetben úgy kell megkeresnünk, hogy α értéke a lehető legnagyobb legyen, a többi betű paraméter. Ez egy elsőéves egyetemi hallgatónak egyszerű házi- (vagy vizsga-) feladat. Aki nem boldogul vele, megnézheti a csatolt Megoldás -ban. Az optimális x képlete nagyon egyszerű, kirándulásra "fejben" is magunkkal vihetjük:

(Csak azért írtuk le három változatban, hogy mindenki a kedvencét vihesse magával.)


    Látókörök

    Színházban sorokban ülünk (ha nem késtünk el), persze jobb a sor közepén ülni, sőt sem az első, sem az utolsó sorban nem szeretek ülni. Miért? Megint a legnagyobb látószöget keresem.
    Hogyan lehetne igazságosan ültetni a nézőket, hogy egy-egy sorban mindenki ugyanolyan jól, vagyis ugyanolyan (látó)szög alatt lássa a színpadot? Középiskolában tanultuk a látókörök tételét: Adott szakaszt (a színpad) adott (rögzített) szög alatt látó pontok mértani helye egy körív. Tehát a széksorokat az alábbi ábra szerint kellene építeni:


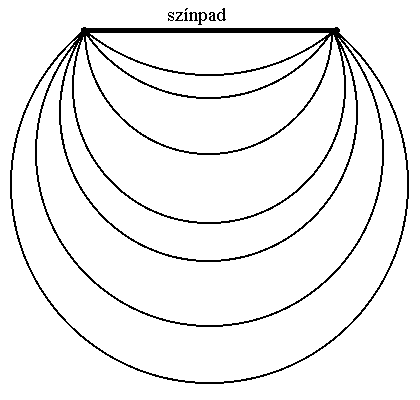
Kicsit furcsa sorok? Szerintem inkább az a fura, hogy a gyakorlatban (már több száz éve) nem így építik a széksorokat! Bizony, az ókori, kör alakú arénák (ahol színdarabokat is előadtak) elrendezése sokkal igazságosabb!


    Meglepő, hogy a látókörök téma milyen sok könyvben szerepel. Íme három:
      Szalkai István: Mindennapi matematika (kézirat),

        Koltay László és a Szerző Analízis I. feladatgyűjteménye, aminek tartalomjegyzékét a Kiadó és a Szerző honlapján is megtalálhatjuk.

    Norbert Herrmann: Mathematik ist überall (Matematika mindenütt), http://www.amazon.de/dp/3486582437/ . . . . Norbert Herrmann honlapjának címe is már önmagáért beszél: http://www.mathematikistueberall.de/










←   16. A Föld gömbölyű                                         18. Fények és árnyak   →




Szalkai István
Pannon Egyetem
Matematika Tanszék
Veszprém
szalkai@almos.uni-pannon.hu
2014.12.03.