← 6. Billeg
8. Tojás belül →
7. A tojás nem törik? (Boltívek)
"Gyengén bánj vele [Vigyázz rá], mint a hímes
tojással!" Tudjuk, hogy nem a hímes festéssel, hanem a tojás héjával
van a gond: a boltból (falusi néni udvarából) is csak nagyon óvatosan
hozzuk haza ezt a finom, de kényes eledelt. (Érdekesség: pár száz évvel
ezelőtt a nagy festők a festékek keveréséhez tojás sárgáját használták
kötőanyagként.)
A baj csak akkor kezdődött, amikor barátunktól egy doboz
fürjtojást kaptunk ajándékba:

(A fürjekről részletesebben olvashatunk a Wikipédián:
Wikipédia: Fürj).
Igaz, hogy ezek csak 2-3 cm tojásocskák, de annál finomabb rántotta lesz
- gondoltuk. Csakhogy alig tudtuk feltörni az apró golyócskákat!
Nem, a héja nem vastagabb a tyúktojásénál, sőt! Anyaga is mindkettőnek
ugyanaz: mész, megkérdeztem egy másik, kémikus barátomat! Az alakja más?
Nem, mindegyiknek tojás alakja van!
Tehát a fürjtojás héja amiatt erősebb a tyúktojásénál,
mert kisebb? Igen: a kisebb tojásnak nagyobb a görbülete
("görbültsége"), hiszen hamarabb meg kell "kerülnie azt a
360o fokot, mert kisebb a kerülete. Igen, egy drótdarabot
(műanyag vonalzót) minnél jobban meggörbítünk, vagyis
nagyobb görbülete lesz, annál kisebb karikát látunk magunk
előtt!
Hogy a nagyobb görbültség miért okoz nagyobb teherbírást
(akár tojáshéjnál, akár diónál vagy papírnál), az alábbi ősrégi, egyszerű
kísérlet segít megérteni. A görbület matematikai definíciója kicsit
bonyolultabb, a
10. Kanyarodunk
fejezetben foglalkozunk vele részletesebben.
7.1. Egy játékos kísérlet
Vegyünk elő egy kis papír vagy rajzlap darabot, esetleg
levelezőlapot (erős kartonpapírt semmi esetre sem!). Mennyi pénzérmét
bír meg egy papír-polc (híd)? Ez attól függ, hogy miként tesszük le a
papírt, mondjuk két könyv közé.
"Természetesen" csak rátesszük:
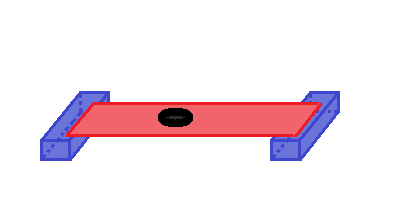
Lehet, hogy így a papírdarab még saját súlyát sem bírja el, lehajlik,
de legjobb esetben is csak egy-két érmét (pl. 100,-Ft) bír el.
Hogyan lehetne másképpen? Például ha ívelten felfelé
hajlítjuk kissé, végeinél esetleg odaszorítjuk a könyvekhez:
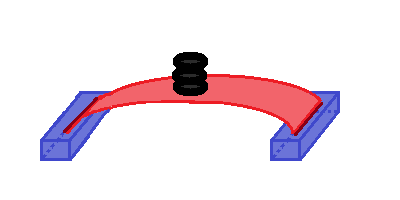
Igen, most már akár egy-két tucat érmét is kibír!
Emlékezzünk csak : amikor nagy folyami hídon
megyünk keresztül gyalog (de autóval is): mennyit kell felfelé majd
utána lefelé mennünk - mert így a vasbeton híd is sokkal több terhet
bír ki - már az alakja miatt is! (A boltívekről az utolsó alfejezetben
még mutatunk néhány gyönyörű képet.)
A boltíves papírhídnál még akár tízszer többet is kibír
a harmonikaszerűen oda-vissza hajtogatott híd:
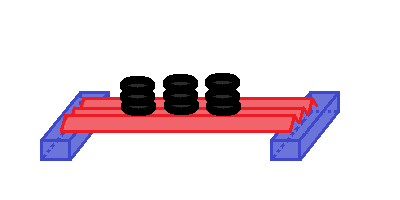
Tessék kipróbálni! A harmonika-papírhíd meglepően sokat kibír!
No, persze a fiatalok, főleg a mérnökjelölt egyetemisták mi mindenre
képesek: tessék alaposan megnézni a fényképeket:
http://se.sze.hu/papirhid-epito-bajnoksag-2013 , például:

Sőt, Franciaországban még "igazi" hidat is építettek
papírból, mely 20 embert is elbírt:

7.2. A gyakorlatban
"Én ugyan a gyakorlatban nem csinálok sem papír-
sem igazi hidat!" - hallom dohogásodat Nyájas Olvasóm! Nem-e?
Hát amikor körültekintően összegyűrt (szakkifejezéssel: kreppelt)
újságpapírt teszünk a törékeny holmi köré a dobozba (első kép):



vagy a cipőnkbe egy kiadós séta,
ének az esőben után (középső kép)!
A kreppelt (gyűrött) papír kicsiben olyan, mint
a hatalmas acél- és faszerkezetű tornyok, hidak, bakonyi kilátók
"össze-vissza" gerendái. Gyönyörködjünk kicsit a portói
Lajos kiráy hídja (Portugália) matematikájában és fizikájában,
melyet ugyanaz az Gustave Eiffel tervezett, mint az 1889. évi
párizsi világkiállításra épített "Eiffel-tornyot" (harmadik kép).
Ugye mindenki hallott már kreppelt papírról,
ruhaanyagról, ágyneműről? Érdekesen puha tapintása van, még az A/4
írópapír is sokkal puhább lesz, ha alaposan meggyűrögetjük, kreppeljük.
(No, hát ezért nem kell vasalni a krepp ágyneműt: már eleve
össze van gyűrve!)


A hajkreppelő eszköznek is figyeljük meg a hullámosító,
harmonikaszerűen hajtogató fogazatát. Bár hajunk kreppelésekor
nem a hajszálak erősítése, teherbírása a célunk (bár a hajfonat
teherbírásáról is mesélhetnék sokat), ha van ilyen eszközünk
otthon, akkor segítségével könnyen hajtogathatjuk a bevezető
kísérletben vizsgált, legerősebb papírhidat is!
A harmonikaszerűen összehajtott, megerősített papírral
nap mint nap találkozunk. Nézzük meg egy erős dobozkarton
(hullámkarton) felépítését:



ráadásul itt a harmonika-papírokat még jobbról-balról meg is ragasztották,
el ne csússzanak, ez megint az erősséget növeli. A papír gyümölcsösládák
több kilogrammot is elbírnak így. Ha esetleg sikerül szétszednünk
(széttépnünk) egy dobozkartont az eredeti papírokra, meg fogunk lepődni:
az A/4 írópapírnál alig vastagabb anyagból áll!
Sőt, újabban sok törékeny eszközt (műszaki-, konyhai-,
egyéb) kreppelt kartonpapírba csomagolnak (habszivacs helyett),
mint a tojástartók anyaga - no, és itt vissza is kanyarodtunk a tojásokhoz!
Ehhez hasonlók a műanyag (sőt néha a vaslemez-)
kannák, nagyméretű tartályok oldalai is:



a hullámosítás szintén az oldalak erősítését szolgálja, mint az autóutak
mellett szaporodó szalagkorlátoknál:

7.3. Még egy játék
A harmonikaszerűen összehajtogatott papírral másutt
is találkoztunk már. Ennek megértéséhez nyomtassuk ki az alábbi "képet"
körülbelül levelezőlap méretben:

majd hajtogassuk oda-vissza harmonikaszerűen úgy, hogy a színes fele
legyen kívül, és természetesen a két (elbújtatott) kép csíkjai között
legyenek a hajtások. Ha most kissé oldalról-felülről megfelelő szögből
nézzük, akkor csak egy MACSKÁT, ellenkező oldalról nézve pedig egy
EGERET látunk! Tessék kipróbálni: óvodás unokatestvért jól el lehet
szórakoztatni vele. Sőt, bármely két azonos méretű képet is kivághatunk
újságból, csíkokra vágva felváltva ragasztunk egy fehét papírra és
máris hajtogathatunk, nézegethetünk kedvünkre.
És ha mindezt nagyon kicsiben (körülbelül
tizedmilliméter hajtásokkal) képezeljük el, akkor előttünk van azon
műanyag gyermekvonalzók "titka", amelyeket kicsit forgatva
egyszer MACSKÁT, máskor EGERET mutatnak! Ugye, milyen ötletes!
Mellékesen a műanyag vonalzók is kissé erősebbek lesznek ezáltal,
ami gyermekeknél nem elhanyagolható.
Ezt a képváltogató vonalzót sokan tévesen
"hologramos" vonalzónak hívják. A hologram egészen más, a
http://www.vilaglex.hu/
címen egészen jó ismertetőt találhatunk a
hologramokról.
A harmonikaszerűen összekevert képekhez
hasonló játékot láthatunk a
Csodák Palotája
interaktív játszóházban:

Forrás:
http://www.csopa.hu/
Itt egy keretben tükörcsíkok és üres hézagok váltakoznak. Két
"játékos" (lehetőleg fiú és lány) ül egymással szemben. Mit látnak?
A tükörcsíkokban saját magukat, míg a hiányzó részeket kitölti a
szemben ülő képe, egész mókásan kiegészítve egymást! Érdemes akár
otthon is kipróbálni!
7.4. Boltívek
Már az ívelt papírhídnál is eszünkbe jutottak a
hidak. Hát persze, a boltív is egy speciális ív
(angolul egyszerűen csak arch["ív"]). A boltívekről részletesen
olvashatunk matematia- és fizika- tankönyvekben, interneten, mint
például a
Wikipédián
vagy a
Wikipedia.org
honlapon. Egy egyszerű számítási mintafeladatot a KöMaL
tesztversenyén találhatunk:
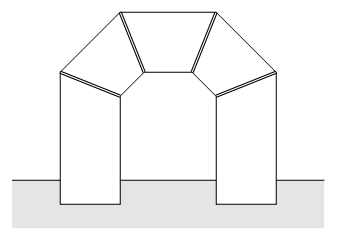
2010. december, fizikai feladatok , 4. feladat a lap alján.
Búcsúzóul már csak pár gyönyörű képet választottunk:
figyeljük meg a műszaki megoldás (apró kövekból áthidalót
építeni egy nagy terem fölött) és az esztétikai szépség
összhangját!


Kairouan(Tunézia)
A párizsi Notre Dame

Csontvári Kosztka Tivadar: Római híd Mostárban (1903)

2010
Képek forrása: Internet
← 6. Billeg
8. Tojás belül →
Szalkai István
Pannon Egyetem
Matematika Tanszék
Veszprém
szalkai@almos.uni-pannon.hu
2014.12.03.

























