← 24. Kémia
Olvasnivalók →
 25. Bűvésztrükkök
25. Bűvésztrükkök
Van jónéhány bűvésztrükk, amely teljesen
automatikus. Ez azt jelenti, hogy a bűvész (kivételesen)
csak azt csinálja, mint amit mond, amit a nézők látnak, a trükk
tényleg "magától" működik. Nem kell kézügyesség, csalás - a csodát
a Természet Törvényei (fizika, kémia, matematika) hozzák létre!
Általában minden természeti jelenséget csodának és trükknek
tartanak az emberek, amíg ésszerű, tapasztalati magyarázatot nem
találnak rá. Mindenki rácsodálkozik a héliumos lufira, felfelé
guruló karikára, radioaktivitásra, automobilra, Internetre, ha
még nem látott ilyesmit! A még fel nem fedezett természeti jelenségek
és törvények már léteznek több, mint egymillió éve, csak
várni kell a felfedezésükig még 5-100-1000 ... évet.
A mindennapjainkban található automatikus gépek
működéséről nagyszerű animációkat találhatunk a
http://animagraffs.com/
honlapon. Mi most csak lakásban elvégezhető
bűvésztrükkökkel foglalkozunk.



25.1. Tea és víz


Már a 24. Egy kis kémia
fejezetben is láttuk: közönséges teába ásványvizet öntve kivilágosodik
a folyadék.
A nézők szeme láttára tüdőnkkel felfújt lufi is lebeg az
üvegtartályban, ha előtte a tartályt széndioxiddal töltöttük meg.
Egy összetört üvegpohár cserepit is nyugodtan beleszórhatjuk
egy "vízzel" teli edénybe, majd az ép poharat egyszerűen kiemeljük belőle,
ha előzőleg az edénybe víz helyett glicerint töltöttünk, és benne
elrejtettünk egy ugyanolyan, ép üvegpoharat.
A tojás is lebeg a vízben, ha előtte sok sót is
tettünk az edénybe (és jól el is kevertük).
A bűvészek rengeteg vegyületet és hatásait ismerik
(talán jobban, mint a vegyészek), havat fakasztanak egy pohárban nyáron,
az ásványvizes palackban
levő víz másodpercenként más színben tündököl, rugalmas kötél hirtelen
megmerevedik és felmászunk rá, a ceruza nem esik le, stb. Nagyon sok
jelenség mindössze csak a természeti törvények miatt látható, még
bűvész sem kell hozzá!
25.2. Párok


Gyermekkorunkban sokszor játszottunk "párosítós kártyával":
mindegyik lapnak van párja. Mindenkinek osztunk öt lapot, majd egyesével
felváltva húzunk a pakliból. Ha a pakli elfogyott, egymástól húzunk. Eközben,
akinek kezében van egy pár mindkét kártyája, azt a párt leteszi maga elé.
Az győz, aki több párt gyűjtött.
A Fekete Pétert általában kivettük, hogy bőgés
ne legyen. Ha csak kettő személy játszik, akkor egy érdekességet vettünk
észre:
Ha a párosítós kártyajátékban a lapok száma
osztható néggyel (vagyis a párok száma osztható kettővel), és csak
ketten játszanak, akkor a végeredmény mindig döntetlen.
Ez könnyen meggondolható, szinte természetes. A játék
második félidejében, vagyis amikor éppen elfogy az asztal közepén levő pakli,
akkor mindegyik, még le nem tett kártya párja a másik játékosnál van. Emiatt
azonban mindkét játékosnál ebben a pillanatban ugyanannyi lap van.
A játék kezdetén mindketten ugyanannyi lapot kaptak, felváltva ugyanannyit húztak,
most ugyanannyi van kezükben, tehát ugyanannyi lapot tettek le az asztalra maguk
elé, vagyis már eddig ugyanannyi párt gyűjtöttek. Így az asztalon levő lapok száma
4-gyel osztható. Mivel eredetileg is 4-gyel osztható volt a lapok száma, ezért
most a játékosok kezeiben levő lapok száma összesen szintén 4-gyel osztható,
fele itt, fele ott. Ezután a játékosok egymástól húznak felváltva, ezért
ugyanannyi párt fognak gyűjteni a játék hátralevő részében is. Ezzel
bebizonyítottuk az észrevételt, vagyis a Tételt.

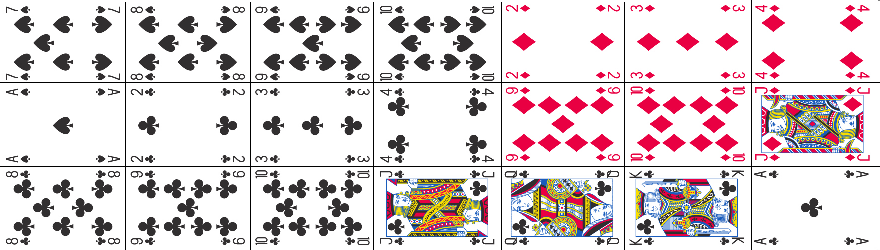
Keressük meg az alábbi négy lap párját az alsó sorban
(megoldásunkat nem árt ellenőrizni!):







25.3. Középen
Előveszek 21 kártyalapot. Megmutatom a lapokat a nézőknek,
egyikük választ egyet, természetesen nem mondja meg nekem. A lapokat egyesével,
színükkel felfelé rakom le az asztalra három csomagba: balra, jobbra, középre,
balra, jobbra, középre, és így tovább. A nézőnek csak annyit kell mondania,
hogy melyik csomagba került a kiválasztott lapja. Ezután egymásra helyezem a
három csomagot: a néző lapját tartalmazó paklit teszem középre. Ezt a
szétosztást és összerakást még kétszer megismétlem! Végül egyszerűen kiterítem
a 21 kártyát színükkel felfelé egy sorba, a néző által megjegyzett lap pedig
mindig a csomag közepén, a 11-dik helyen lesz!
A mutatvány teljesen automatikus, csak az kell csinálni,
ami le van írva - Nyájas Olvasóm, tessék most kipróbálni! Amikor a három
kis csomagot legelőször összeszedjük, akkor néző által kiválasztott kártya
a középső csomagban volt, vagyis az egyesített csomagban a 8. és 14. hely
között valahol. A következő "terítéskor" először az előtte levő 7 kártyát két
rétegben letesszük, ezután jön a néző kártyája, legfeljebb a 3.rétegben,
majd újabb két réteg kártya. Ez azt jelenti, hogy a második összeszedés
után kártyánk már biztosan a 10. és 12. hely között bújik meg.
Hasonlóan, a nagy csomag harmadik szétosztásakor már
legalább 3-3 réteg kártya van a néző lapja alatt és felett (az asztalon).
Tehát a legutolsó összeszedéskor legalább 7+3 kártya kerül a kiválasztott
lap alá és fölé, ez pedig csak úgy lehet, hogy a keresett lap pontosan
a 11. helyen van!
Ha a fenti gondolatmenet kicsit bonyolultnak hangzik, akkor
a kiválasztott kártya helyett tegyünk egy, a többi laptól nagyon elütő
színű kartonpapírt, és figyeljük meg annak mozgását!
Ez a mutatvány 21 helyett tetszőleges páratlan számú
kártyára is működik, csak nem háromszor, hanem többször kell szétosztanunk
és összeszednünk. Részleteket Szalkai Balázs és a Szerző
Kártyajátékok és bűvésztrükkök cikkében olvashatunk (megjelent a
Polygon folyóirat XXI. számának 89-100. oldalain, 2013-ban).
25.4. A SET -kártya
Bizonyára már sokan találkoztatok a SET kártyával,
iskolások között népszerű. Attól nem kell megijedni, hogy a SET szó
a matematikában halmazt jelent, mert a hétköznapi életben
csoportot, készletet is jelent.
Marsha Jean Falco genetikus 1974-ben
Cambridge-ben dolgozott, a génkombinációk rövidített jeleit kis
kártyákra írta és így rendszerezte. Azonos, vagy éppen különböző mintájú
kártyákat keresett. Ebből alakult ki a játék, melyet először
csak barátaival és családtagjaival játszott, míg 1991-ben sikerrel
bevezette a játékpiacra.
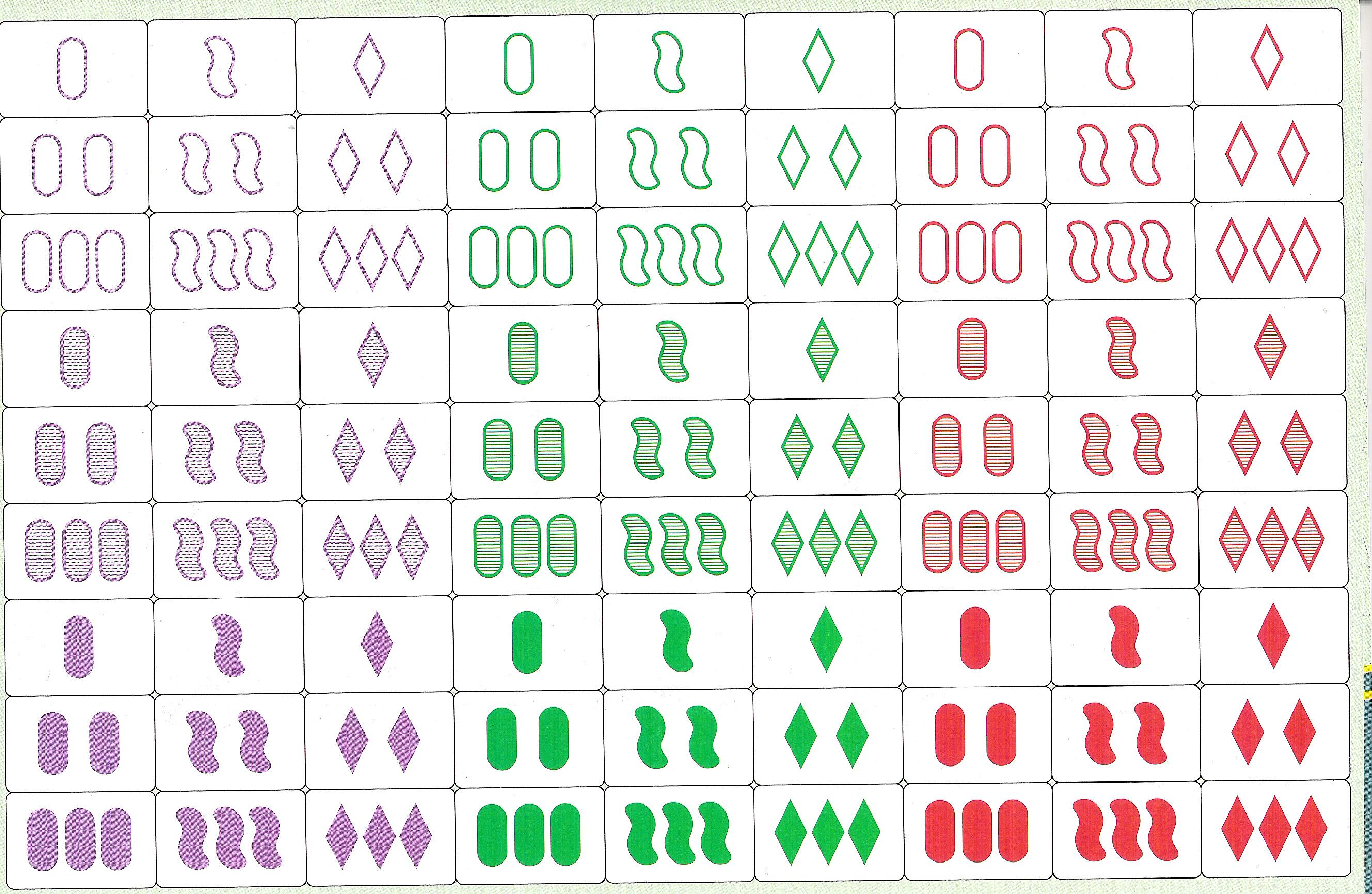
A játékot két vagy több játékossal, a fent látható
lapokkal játszhatjuk: minden kártyán 1, 2 vagy 3 rombusz, hullám vagy
ovális forma látható, piros, zöld vagy lila színben, csíkos, üres vagy
teli kitöltéssel. Kezdetben 12 kártyát helyezünk az asztalra színnel
felfelé, majd mindenki elkezdi vizsgálni őket, SET-et keresve.
SET-et három olyan kártya alkot, melyek esetében
mind a négy tulajdonságra teljesül, hogy vagy mindhárom kártya
ugyanolyan, vagy mindhárom különböző. Például SET-et alkotnak
a következők:
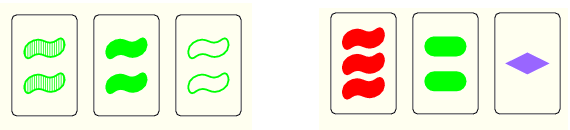
Ha valaki talált egy SET-et, akkor azt elveszi, és a kártyák helyére
újabb kártyák kerülnek. Ha az asztalon lévő kártyák között nincs SET,
akkor újabb három kártya kerül az asztalra.
A játéknak akkor van vége, ha elfogynak a lapok, vagy ha már
csak az asztalon vannak kártyák, és ezek között nincs SET. Az a
játékos nyer, aki a legtöbb SET-et találta meg.
A játékról és annak matematikai vonatkozásairól
Deme-Farkas Rita: Variációk a SET témájára,
KöMaL 2008/2, 71-75.oldal, vagy az alábbi honlapon olvashatunk:
http://www.komal.hu/cikkek/2008-02/SET.h.shtml .
25.5. Csodagömb
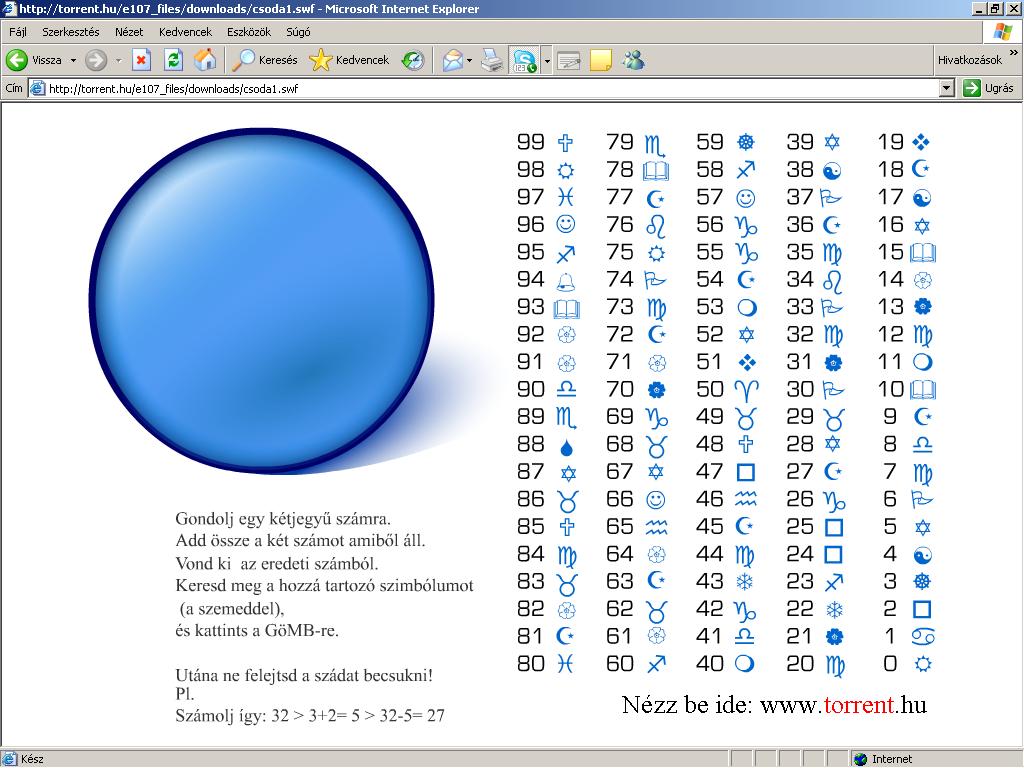
Interneten hamar megtaláljuk ükapáink
kedvenc játékának önműködő változatát: elég a "Csodagömb"
szóra keresnünk, például
http://www.mathematika.hu/viewpage.php?page_id=100
" Gondolj egy kétjegyű számra. Add össze a két
számjegyet amiből áll. Vond ki az eredeti számból. Például számolj
így: 32 ⇒ 3+2=5 ⇒ 32-5=27. Keresd
meg a hozzá tartozó szimbólumot (a szemeddel), és kattints a GÖMB -re.
Utána ne felejtsd a szádat becsukni! "
... és az alábbi magyarázatot elolvasni ... !
Magyarázat: Bármelyik számból kivonva
számjegyeinek összegét, mindig 9 -cel osztható számot kapunk:
(10a+b)-(a+b) = 9a . Nézzük meg alaposabban a
Csodagömb ábráit: minden 9-cel osztható számnál
ugyanaz a jel szerepel (kivéve persze 0,90 és
99), és a gömbre kattintva is ugyanezez
a jel tűnik elő! Tehát akármelyik számra is gondolunk, mindig
a 9-cel osztható jel fog előtűnni! Próbáljuk csak
ki!
 Sorry, ezt a trükköt már Grätzer József
is ismerte, aki Karinthy Frigyes személyi titkára volt
az 1920-as években. Valószínűleg már ők is dédapáiktól hallották.
Ugyanis, például a SICC - Szórakoztató Időtöltések, Cseles
Csalafintaságok (1935) könyvben olvashatunk hasonló
lélegzetelállító fejszámolási mutatványokat, például:
Sorry, ezt a trükköt már Grätzer József
is ismerte, aki Karinthy Frigyes személyi titkára volt
az 1920-as években. Valószínűleg már ők is dédapáiktól hallották.
Ugyanis, például a SICC - Szórakoztató Időtöltések, Cseles
Csalafintaságok (1935) könyvben olvashatunk hasonló
lélegzetelállító fejszámolási mutatványokat, például:
"Gondolj egy számot 10 és 99 között!
Cseréld meg jegyeit! Vond ki a kisebb számot a nagyobból. Ha
egyik jegyét megmondod a végeredménynek, akkor én megmondom a
másik jegyet!"
No, mi a különbség? Semmi! Nincs új a Nap alatt!
Többjegyű számokra szintén igaz, hogy a számból jegyeinek összegét
kivonva 9-cel osztható számot kapunk, ez házi feladat.
25.6. Egy négyzet hányzik
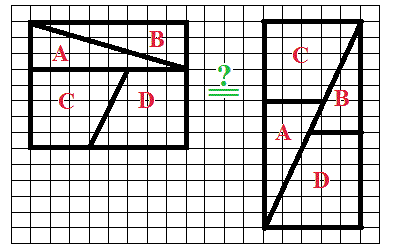
Az ábrán minden látszik: a bal- és a jobboldali
ábrákon az A,B,C,D részek páronként egybevágóak, szemmel
láthatóan szépen illeszkednek egymáshoz, mégis baloldalon
8*8=64, a jobboldalon 5*13=65
a területük összege! Bár ezt a "trükköt" sok matematikakönyvben
megtalálhatjuk, én mégis Veszprém megye szülötte Galambos
Ferenc világhírű bűvésztől láttam először. Pedig a
fenti A,B,C,D részek
igazi kis falapok voltak, izgatottan kerestük az elvezett
négyzetet az asztal alatt - persze a bűvész úr mindig
másvalakinek a zsebében vélte megtalálni. Ajánlom még a következő
honlapokat is:
http://buvesz.blog.hu/2009/10/31/galambos és
http://www.galambosmagic.hu/ .
Magyarázat: Szemünkkel valóban nem
veszük észre, de az A,B,C,D részek a jobboldali
ábrán nem teljesen érintkeznek: (középiskolai) matemamatiki
módszerekkel kiszámolható, hogy mekkora rés van közöttük.
Nagyon vékony, de pontosan 1 négyzetnyi!
Az alábbi, hasonló átdarabolás a KöMaL
honlapjáról való:
http://www.komal.hu/cikkek/trukkos/atdarab/atdarab.h.shtml
:
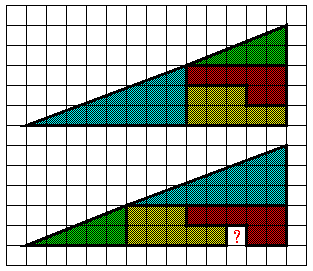
25.7. Maria Prope Vivet Mutuo

Ezeket a varázsszavakat és a mutatványt a 90 éves
Mikó Ernő nagypapától hallottuk. Sajnos csak "francia" kártyával
tudjuk előadni, "magyar" kártyával nem.
Leteszünk az asztalra 20 kártyalapot: 10 figurát,
mindegyikből kettőt-kettőt, a szín most nem érdekes, négy sorban és öt
oszlopban. Egy néző választ tetszőleges figurát (pl. Király), de nem
árulja el. Csak annyit kérdezünk, hogy melyik sorban vagy sorokban
szerepel ez a figura, és azonnal kitaláljuk, hogy melyik figurát
választotta.
A 10 figura két-két példányban nem olyan sok, egy vagy
két sorban meg lehet könnyen találni az azonosakat egy jó fejű bűvésznek,
mondhatja bárki. De mi van akkor, ha véletlenül két figura is megoldás,
vagyis a néző által mutatott sor(ok)ban kettő figura is szerepel
kétszer? Tehát a lapokat nem lehet akárhogyan letenni az asztalra!
Csak szilárd matematikai alapokon álló varázsszavak
után:
 Az asztalra mindegyik betű helyett egy neki megfelelő
figurát teszünk. A táblázat úgy van megszerkesztve, hogy mindegyik figura
egyértelműen kitalálható legyen a néző által megmutatott sorból vagy
sorokból. A varázsigék a táblázat könnyebb megjegyzéséhez kellenek:
mindegyik betű egy-egy figurát jelent! Például:
Az asztalra mindegyik betű helyett egy neki megfelelő
figurát teszünk. A táblázat úgy van megszerkesztve, hogy mindegyik figura
egyértelműen kitalálható legyen a néző által megmutatott sorból vagy
sorokból. A varázsigék a táblázat könnyebb megjegyzéséhez kellenek:
mindegyik betű egy-egy figurát jelent! Például:

Általános kérdés: El lehet-e helyezni n
sor mindegyikében m kártyát úgy, hogy mindegyik figurából 2-2 van
az asztalon, és mindegyik figurát egyértelműen jellemez az a két
sor, amelyekben ennek a figurának a két lapja található? A
választ (matematikai levezetéssel) Szalkai Balázs és a
Szerző
Kártyajátékok és bűvésztrükkök cikkében olvashatunk (megjelent a
Polygon folyóirat XXI. számának 89-100. oldalain, 2013-ban).
25.8. Négy kartonpapír
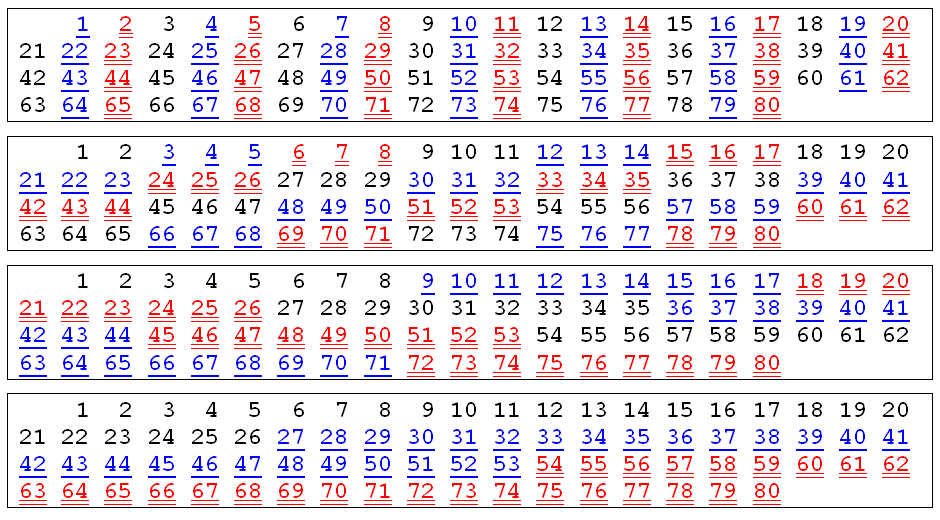
Megkérem játékostársamat, hogy gondoljon egy számra
0-tól 80-ig, de ne mondja meg, csak azt, hogy a fenti négy kartonpapír
melyikén és milyen színnel találta meg a választott számot. Ezután egy
pillanat alatt kitalálom a számot!
A nagyobb hatás érdekében a számokat össze-vissza is
lehet a papírokra írni (persze a színkódok megtartásával), sőt a
fekete számokat nem is kell felírnunk a papírokra.
Magyarázat: Az első táblázatban hármasával
ismétlődnek a színek, a második táblázatban már három azonos szín
követi egymást, a harmadik táblázatban kilenc, a negyedikben pedig
már 27 azonos szín követi egymást. A felsorolt számok éppen 3 hatványai,
tehát a fekete-kék-piros színek a választott szám számjegyei a
a hármas számrendszerben!
Összefoglalva: Ha egy kartonpapíron FEKETE
színnel szerepel a szám, akkor azt a papírt nem kell tekintenünk. Ha egy
papíron a szám KÉK színnel szerepel, akkor
azon a papíron szereplő legelső KÉK számot jegyezzük meg, ha pedig
egy papíron a választott szám PIROS színnel
szerepel, akkor azon a papíron szereplő legelső PIROS számot
jegyezzük meg. Ezeket a megjegyzett számokat összeadva kapjuk a
néző által választott számot!
A mutatványt "természetesen" könnyen általánosítható
80-nál több számra, illetve akárhány színre (azaz bármely alapú
számrendszerre), a részleteket Szalkai Balázs és a
Szerző
Kártyajátékok és bűvésztrükkök cikkében olvashatjuk (megjelent a
Polygon folyóirat XXI. számának 89-100. oldalain, 2013-ban).
25.9. Varázsdiók

Vegyünk elő három kisméretű tárgyat, mondjuk ceruza,
kulcs, bicska. Az asztalra teszünk 24 diót, amiből három
önként jelentkezőnek 1 , 2 illetve 3 szemet adunk.
Megkérjük őket, hogy távollétünkben rejtsenek el zsebükbe egy-egy
tárgyat. Továbbá: aki a ceruzát dugta el, vegyen el
még ugyanannyi diót, mint amennyit adtunk neki, a kulcs
"gazdája" kétszer annyit vegyen el mint amennyit tőlünk kapott,
míg a bicskánkat rejtegető személy dióinak négyszeresét
vegye még el.
A szobába visszatérve csak rápillantunk az asztalon
levő diókra, megszámoljuk őket, és kitaláljuk, kinél milyen tárgy van!
A megoldás kulcsát, azt hiszem, nem kell
részleteznem: minden lehetőség (melyik személy mit dugott el) esetén
más-más az asztalon maradt diók száma. Ezt kis táblázatban könnyen ki
is mutathatjuk, sőt a táblázatot kívülről is tanácsos megtanulnunk!
(Házi feladat: a fenti képen számoljuk meg a diókat, és találjuk
ki, hogy kinél van a golyóstoll?)
A fenti táblázat is, és a feladat általánosítása
is a különböző alapú számrendszerek segítségével lehetséges,
erről bővebben a Szerző következő cikkében olvashatunk:
Számrendszerek alkalmazásáról , Polygon (Szeged), 7.kötet
(1997), 85-88.oldal. A cikkben felvetett matematikai
kérdés máig is megoldatlan!
25.10. Négy és az ötödik
Az 52 lapos csomagból egy néző kiválaszt tetszőleges
ötöt és átadja nekem, a maradék kártyákat félreteszi. Én a kapott öt
kártya közül egyet zsebre teszek, a másik négyet pedig leragasztom egy
borítékba. A borítékot egy másik néző átviszi a szomszéd szobában
várakozó társamnak, aki kibontja a borítékot, és megmondja, melyik
volt az ötödik kártya amit én zsebre tettem. Hogyan?
A feladat és megoldása eredetileg van Lint,J.H.
és Wilson,R.M. 2001-ben megjelent könyvéből való, figyelmemet
Hujter Mihály barátom hívta fel. A megoldás bár középiskolás
szintű, de kicsit hosszú, ezért az érdeklődőknek csak
Szalkai Balázs és a Szerző
Kártyajátékok és bűvésztrükkök című, a Polygon
folyóirat XXI. száma (2013), 89-100. oldalain megjelent cikkét
ajánljuk.
25.11. Hókuszpókusz
Végül eláruljuk ennek a varázsigének az eredetét.
Kedves barátom, Bak Tamás atya fedte fel előttem. Alig száz évvel
ezelőtt ugyanis minden mise latin nyelven folyt, és átváltoztatáskor,
az ostya felmutatásakor a pap (néha kicsit halkan) idézte:
"Hoc est corpus meus!" (=Íme, az én testem), amit nem nehéz
hókusz-pókusz-nak érteni, főleg nagyotthalló nénikék és bácsikák
esetében.
A Szerző Mindennapi matematika könyvében
is találunk bűvészetről matematikai fejtegetéseket, sajnos a könyv még
kiadatlan, tartalomjegyzéke:
Mindennapi matematika .
Néhány bűvészettel foglalkozó oldal azonban olvasható:
http://buvesz.trukkok.hu/
http://www.jokermagic.com/home.php?nyelv=0
http://kezdo-buveszet.mindenkilapja.hu/html/19365621/render/kartyatrukkok-megold
https://www.youtube.com/watch?v=ldBhVcDVBzs
(Eltűntem!)

Képek forrása: Internet, Szalkai Évi és a Szerző.
← 24. Kémia
Olvasnivalók →
Szalkai István
Pannon Egyetem
Matematika Tanszék
Veszprém
szalkai@almos.uni-pannon.hu
2014.12.03.



















 Sorry, ezt a trükköt már Grätzer József
is ismerte, aki Karinthy Frigyes személyi titkára volt
az 1920-as években. Valószínűleg már ők is dédapáiktól hallották.
Ugyanis, például a SICC - Szórakoztató Időtöltések, Cseles
Csalafintaságok (1935) könyvben olvashatunk hasonló
lélegzetelállító fejszámolási mutatványokat, például:
Sorry, ezt a trükköt már Grätzer József
is ismerte, aki Karinthy Frigyes személyi titkára volt
az 1920-as években. Valószínűleg már ők is dédapáiktól hallották.
Ugyanis, például a SICC - Szórakoztató Időtöltések, Cseles
Csalafintaságok (1935) könyvben olvashatunk hasonló
lélegzetelállító fejszámolási mutatványokat, például: 






